Buildings Area Density: 0.6#

1. Project Description#

The current study numerically reproduces the experiment 103c13 from the Tokyo Polytechnic University (TPU) Aerodynamic Database with AeroSim’s CFD solver.

A low-rise building with \(B \times W \times H\) dimensions:

is positioned in a wind tunnel setup with 184 pressure probes distributed over its surface:

The target model was positioned at the center of a turnable of 200m diameter, in full scale, with the surrounding buildings regularly arranged within its radius:

To which the density of buildings is determined by an area density coefficient

\[\mathrm{C_{A}}=\mathrm{\frac{area\,occupied\,by\,the\,buildings}{area\,of\,site}}=\frac{BW}{D_{1}D_{2}}\]

Which for the current case is \(\mathrm{C_{A}}=0.1\).

The wind directions chosen to be simulated were:

Wind Directions#
Wind direction	0 \(^\circ\)	23 \(^\circ\)	45 \(^\circ\)	68 \(^\circ\)	90 \(^\circ\)

1. Simulation Setup#

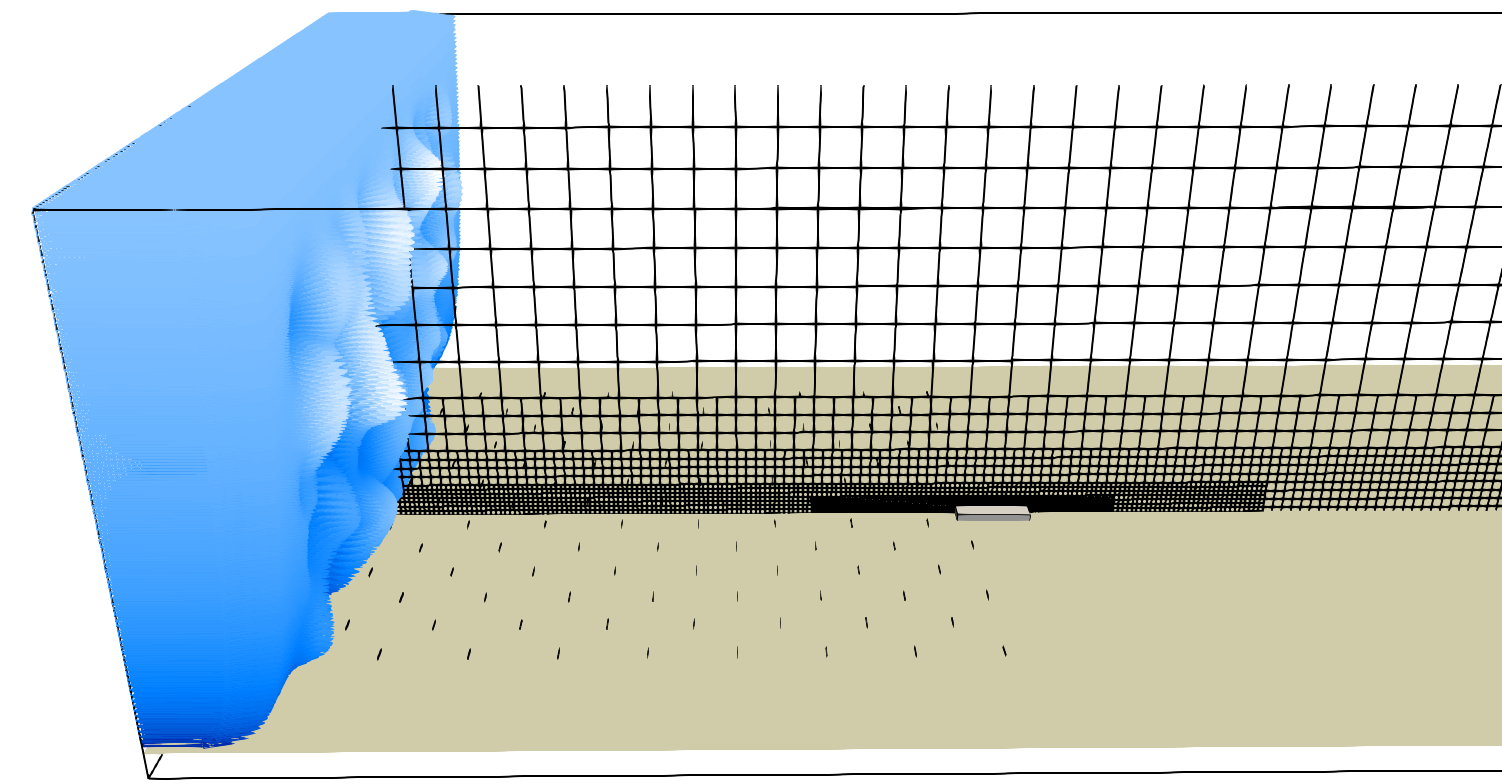
The Synthetic Eddy Method (SEM) boundary condition is applied at the inlet of the computational domain. Solid fins are distributed across the floor to ensure the desired velocity and turbulence profiles during flow development length. A Neumann boundary condition is applied at the remaining boundaries.

The building is positioned \(118H\) from inlet, and 6 grid refinement levels (\(lvl\,0\) to \(lvl\,5\)) were adopted:

A 1:2 refinement ratio is estabilished between levels, and the simulation parameters at grid \(lvl\,5\) were:

Dimensionless Parameters#
\(\boldsymbol{\Delta x/B}\) (spatial resolution)	1.25e-02
\(\boldsymbol{\Delta t/CTS}\) (temporal resolution)	7.72e-04
exports/\(\boldsymbol{CTS}\) (pressure acquisition frequency)	1.00e+01
\(\boldsymbol{T/CTS}\) (statistical sample size)	1.40e+03
\(\boldsymbol{Re_{B}=U_{H}B/\nu}\)	6.18e+04

The equivalent parameters in full scale are:

Full-scale Parameters#
\(\boldsymbol{\Delta x[m]}\)	0.12
\(\boldsymbol{\Delta t[ms]}\)	0.33
\(\boldsymbol{f[Hz]}\)	23.40
\(\boldsymbol{T[s]}\)	600.00

The computational resources required were:

Computational Resources#
Device	NVIDIA RTX A5500	NVIDIA RTX A5500	NVIDIA RTX A5500	NVIDIA A10G	NVIDIA RTX A5500
Wind direction	0 \(^\circ\)	23 \(^\circ\)	45 \(^\circ\)	68 \(^\circ\)	90 \(^\circ\)
Node count (million)	123.39	123.67	123.58	123.67	123.39
Allocated memory (Gb)	18.43	18.47	18.45	18.46	18.41
Ellapsed time (h)	44.75	44.96	44.81	54.52	43.09

3. Inflow#

An empty domain simulation is performed to measure the incident velocity and turbulence profiles. A probe line is placed at the position where the building will be located. The average velocities used for calculating the pressure coefficient and convective time scale are taken from this simulation.

Wind Profiles#

Wind Spectra#

The power spectral density of the velocity components at height \(H\) are compared with theoretical Von Kármán curves to validate the atmospheric flow.

4. Results: Local Statistics#

The pressure coefficient is calculated using the velocity at the building height \(H\) and the reference pressure measured from a position far above the building. The same statistical processing of the pressure coefficient \(C_{p}\) at each probe position is performed for both experimental and numerical data:

A sample of size (\(T / CTS\)) is evaluated over moving averages of the original signals, with window size of 3s.

The processed data is subdivided in 10 intervals, from which the minimum and maximum values will be taken for each.

Those min/max values are fitted to a Gumbel distribution.

The shape parameters from Gubel distribution are then rescaled to 3600s.

Scatter on Points Statistics#

The deviation between numerical and experimental data is quantified using the mean absolute error (MAE) and the normalized mean absolute error (NMAE):

\[\mathrm{MAE} = \frac{1}{N_{\mathrm{probes}}}\sum_{i=1}^{N_{\mathrm{probes}}}|q^{\left(i\right)}_{\mathrm{EXP}}-q^{\left(i\right)}_{\mathrm{NUM}}|\]

\[\mathrm{NMAE} = \frac{1}{N_{\mathrm{probes}}}\sum_{i=1}^{N_{\mathrm{probes}}}\frac{|q^{\left(i\right)}_{\mathrm{EXP}}-q^{\left(i\right)}_{\mathrm{NUM}}|}{\left[q^{\left(\mathrm{max}\right)}_{\mathrm{EXP}}-q^{\left(\mathrm{min}\right)}_{\mathrm{EXP}}\right]}\times 100\]