PA Residential Building

PA Residential Building#

PA Residential Building

1. Project Description#

The current study numerically reproduces a wind tunnel assessment of high-rise building with urban surroundings. The project was measured in a wind tunnel facility. The time histories of forces-by-floor were provided to us, and serve as a basis for comparison

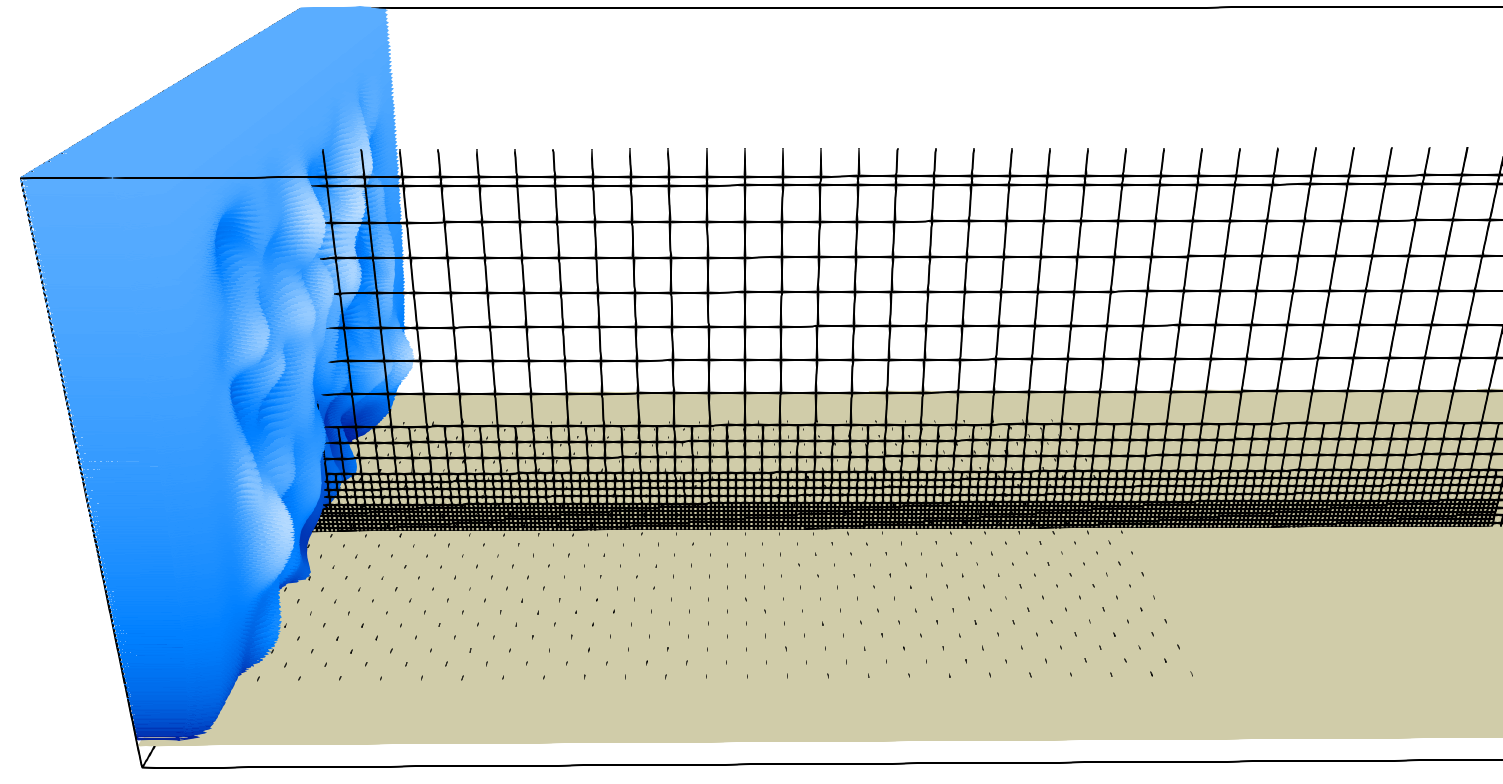
The horizontal reference width of the main building is \(B=45.6\mathrm{m}\) and its geometry is shown below:

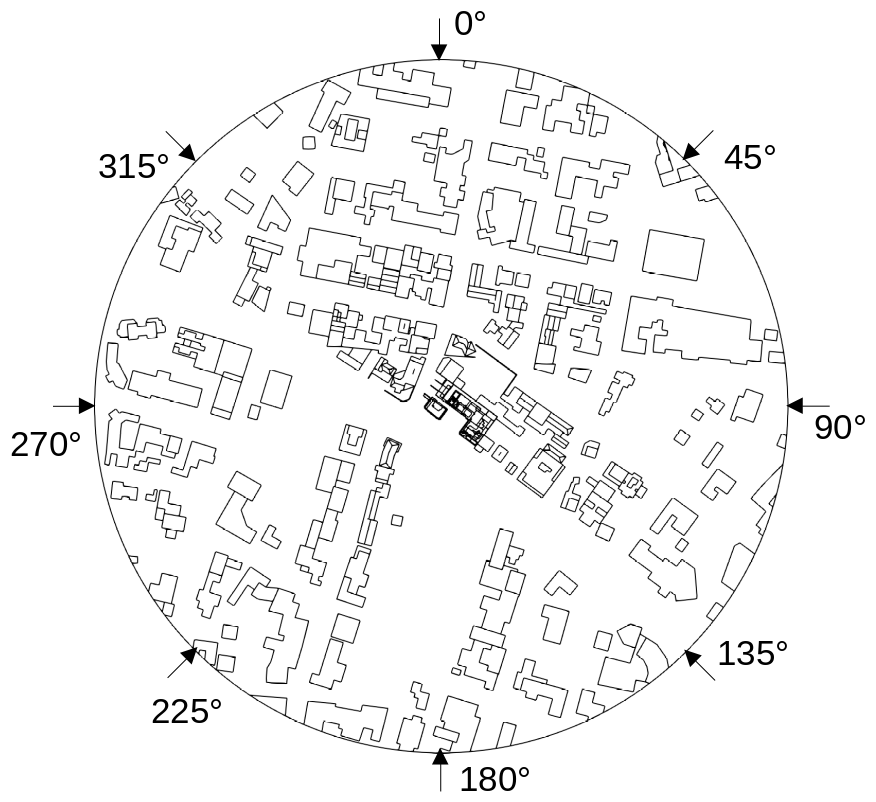
Building Geometry

The wind directions chosen to be simulated were:

Wind Directions#

Wind direction

0 \(^\circ\)

40 \(^\circ\)

90 \(^\circ\)

130 \(^\circ\)

180 \(^\circ\)

220 \(^\circ\)

270 \(^\circ\)

310 \(^\circ\)

With the coordinate system

Building Geometry

1. Simulation Setup#

The Synthetic Eddy Method (SEM) boundary condition is applied at the inlet of the computational domain. Solid fins are distributed across the floor to ensure the desired velocity and turbulence profiles at the test section. A Neumann boundary condition is applied at the remaining boundaries.

The building is positioned \(6H\) from inlet, and 6 grid refinement levels (\(lvl\,0\) to \(lvl\,5\)) were adopted:

Computational Grid

A 1:2 refinement ratio is estabilished between levels, and the simulation parameters at the building level were:

Dimensionless Parameters#

\(\boldsymbol{\Delta x/B}\) (spatial resolution)

6.85e-03

\(\boldsymbol{\Delta t/CTS}\) (temporal resolution)

4.53e-04

exports/\(\boldsymbol{CTS}\) (pressure acquisition frequency)

1.00e+01

\(\boldsymbol{T/CTS}\) (statistical sample size)

1.04e+03

\(\boldsymbol{Re_{B}=U_{H}H/\nu}\)

7.48e+04

The equivalent parameters in full-scale are:

Full-scale Parameters#

\(\boldsymbol{\Delta x[m]}\)

0.31

\(\boldsymbol{\Delta t[ms]}\)

0.45

\(\boldsymbol{f[Hz]}\)

9.98

\(\boldsymbol{T[s]}\)

1046.56

The computational resources required were:

Computational Resources#

Device

Wind direction

Node count (million)

Allocated memory (Gb)

Ellapsed time (h)

NVIDIA A10G

0 \(^\circ\)

122.02

14.76

94.18

NVIDIA A10G

40 \(^\circ\)

127.84

15.41

93.26

NVIDIA A10G

90 \(^\circ\)

119.29

14.45

89.08

NVIDIA A10G

130 \(^\circ\)

127.80

15.41

88.01

NVIDIA A10G

180 \(^\circ\)

122.02

14.75

86.53

NVIDIA A10G

220 \(^\circ\)

128.41

15.47

85.47

NVIDIA A10G

270 \(^\circ\)

120.79

14.61

94.32

NVIDIA A10G

310 \(^\circ\)

128.37

15.46

91.80

3. Inflow#

An empty domain simulation is performed to measure the mean velocity and turbulence profiles. A probe line is placed at the position where the building will be located. The mean velocities used for calculating the pressure coefficient and convective time scale are taken from this simulation.

Wind Profiles#

Inflow Profile

Wind Spectra#

The power spectral density of the velocity components at height \(H\) are compared with theoretical Von Kármán curves to validate the atmospheric flow.

Inflow Spectrum

4. Results: Global Statistics#

The wind effect on the solid building is measured through force and moment coefficients. The building is divided in 76 floors. The force coefficient is calculated as:

(1)#\[C_{f\alpha} = \frac{1}{B H}\sum_{i\,\in\,\mathrm{floor}} C_{p, i} A_{i}n_{i\alpha}\]

where \(A_{i}\) is the tributary area.

For the peak values, the following procedure was applied for both datasets (numerical experimental):

  • The sample is subdivided in sub-samples of duration \(T\), and a 3s moving-average is applied to all sub-samples.

  • The smoothed sub-samples are divided in 10 intervals, from which the minimum and maximum values are taken.

  • The max/min values are fitted into a Gumbel distribution, and the mode \(U\) is rescaled to a duration of 1h.

  • A non-excedence probability of 78% is considered for the extreme values.

Force Coefficient - Mean and Peak#

Mean and Peaks 000
Mean and Peaks 030
Mean and Peaks 090
Mean and Peaks 120
Mean and Peaks 180
Mean and Peaks 210
Mean and Peaks 270
Mean and Peaks 300

Force Coefficient - RMS#

RMS 000
RMS 030
RMS 090
RMS 120
RMS 180
RMS 210
RMS 270
RMS 300

Force Coefficient - Spectrum#

Cfx Spectra 000
Cfy Spectra 000
Cmz Spectra 000
Cfx Spectra 030
Cfy Spectra 030
Cmz Spectra 030
Cfx Spectra 090
Cfy Spectra 090
Cmz Spectra 090
Cfx Spectra 120
Cfy Spectra 120
Cmz Spectra 120
Cfx Spectra 180
Cfy Spectra 180
Cmz Spectra 180
Cfx Spectra 210
Cfy Spectra 210
Cmz Spectra 210
Cfx Spectra 270
Cfy Spectra 270
Cmz Spectra 270
Cfx Spectra 300
Cfy Spectra 300
Cmz Spectra 300

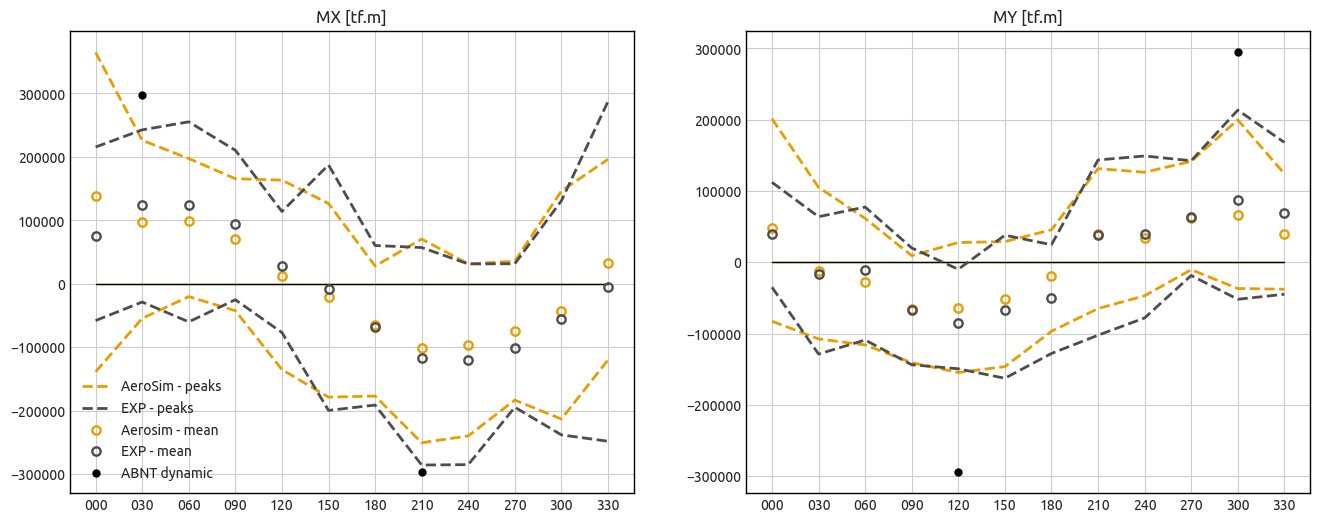
Global Loads#

The static approach for the calculation of peak moments is given by:

(2)#\[R = \bar{R} + g \sigma_{R}\]

where \(\sigma\) is the root-mean-square and we use a peak factor \(g=3\) in the current analysis.

In the dynamic approach, the structural properties must be considered, and \(\sigma_{R}\) is broken in a background component \(\sigma_{B}\), and a resonant component \(\sigma_{RE}\), which results:

(3)#\[R = \bar{R} + g \sqrt{\sigma_{B}^{2}+\sigma_{RE}^{2}}\]

The background parcel is given by:

(4)#\[\sigma_{B}=\frac{\sigma_{F}}{K}\]

and the resonant by:

(5)#\[\sigma_{RE}=\sqrt{\frac{\pi}{4}+\frac{1}{\xi_{s}+\xi_{B}}\frac{f_{0}S_{F}\left(f_{0}\right)}{K^{2}}}\]

where \(\sigma_{F}\) is the root-mean-square of the generalized force, \(K\) is the generalized stiffness (determined from natural frequency and generalized mass), \(\xi_{S}\) and \(\xi_{B}\) are the structural and aerodynamic damping, and \(S_{F}\left(f_{0}\right)\) the power spectrum of the generalized force at the natural frequency \(f_{0}\).

We consider \(\xi_{S}=0.02\) and \(\xi_{B}=0\). The results for the static and dynamic responses for the bending moments is shown below:

Global Loads

Execution Notes#

Execution Notes#

Execution Date (YYYY-MM-DD)

2025-3-7

Solver Version

1.6.18

Changelog#

  • 19 Dez 2024: Added case

Contents